Základní rozdělení
Racionální funkce je každá funkce daná ve tvaru:
Polynomická funkce je každá funkce ve tvaru
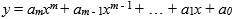
kde m je přirozené číslo.
Definičním oborem každé polynomické funkce je množina R.
Příkladem polynomické funkce jsou lineární a kvadratická funkce.
funkce konstantní:
Je to speciální případ lineární funkce (f: y = ax + b), kde a = 0 a bÎR, tj. funkce f: y = b.
Df = R, Hf = {b}, grafem je přímka rovnoběžná s osou x a procházející bodem [0; b], není rostoucí ani klesající, je omezená, v každém x Î Df má maximum i minimum.
lineární funkce:
Lineární funkce je každá funkce, která je dána předpisem f: y = ax + b, kde a, bÎR.
Jejím grafem je přímka.
Rozdělení podle koeficientu a:
a = 0 - konstantní funkce
a > 0 - Df = R, Hf = R, grafem je přímka procházející bodem [0; b], je rostoucí v celém Df a tedy prostá, není shora ani zdola omezená, nemá maximum ani minimum.
a < 0 - Df = R, Hf = R, grafem je přímka procházející bodem [0; b], je klesající v celém Df a tedy prostá, není shora ani zdola omezená, nemá maximum ani minimum.
Grafy lineárních funkcí:
funkce s absolutní hodnotou:
Absolutní hodnota reálného čísla a je číslo |a|, pro které platí:
je-li a ³ 0, je |a| = a
je-li a < 0, je |a| = -a
Pro každé a Î R je tedy |a| ³ 0, je-li a ¹ 0, pak je |a| > 0, |0| = 0.
Každému reálnému číslu je podle definice přiřazena jednoznačně jeho absolutní hodnota. Získáváme tak funkci na množině R danou předpisem y = |x|, hovoříme o funkci absolutní hodnota.
Graf funkce absolutní hodnota (posouvání základního grafu po osách):

kvadratická funkce:
Kvadratická funkce je každá funkce, která je dána předpisem f: y = ax2 + bx + c, kde a, b, c Î R a a ¹ 0.
Jejím grafem je parabola, osa paraboly je rovnoběžná s osou y, průsečík paraboly a osy paraboly je vrchol V paraboly.
Rozdělení podle koeficientu a:
( a = 0 - lineární funkce)
mocninné funkce s přirozeným exponentem:
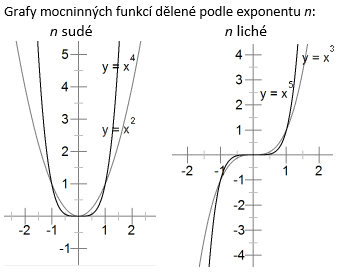
Mocninná funkce s přirozeným exponentem (mocnitelem) je funkce určená předpisem f: y = xn , kde n Î N, Df = R.
Rozdělení podle mocnitele n:
n sudé - Df = R, Hf = á0, ¥), je to funkce sudá, je zdola omezená, shora není omezená, pro x Î (-¥,0ñ je klesající, pro x Îá0, ¥) je rostoucí, má minimum v bodě [0; 0], maximum nemá, není prostá.
n liché - Df = R, Hf = R, je to funkce lichá, není shora ani zdola omezená, je rostoucí v celém Df, nemá maximum ani minimum, je prostá.